
Abstract
How can we know whether new mechanistic interpretability methods achieve real improvements? In pursuit of meaningful and lasting evaluation standards, we propose MIB, a Mechanistic Interpretability Benchmark with two tracks spanning four tasks and five models. MIB favors methods that precisely and concisely recover relevant causal pathways or specific causal variables in neural language models. The circuit localization track compares methods that locate the model components—and connections between them—most important for performing a task (e.g., attribution patching or information flow routes). The causal variable localization track compares methods that featurize a hidden vector, e.g., sparse autoencoders (SAE) or distributed alignment search (DAS), and locate model features for a causal variable relevant to the task. Using MIB, we find that attribution and mask optimization methods perform best on circuit localization. For causal variable localization, we find that the supervised DAS method performs best, while SAEs features are not better than neurons, i.e., standard dimensions of hidden vectors. These findings illustrate that MIB enables meaningful comparisons of MI methods, and increases our confidence that there has been real progress in the field.
Key Contributions
- New metrics: Two integrated faithfulness metrics for evaluating circuit discovery methods
- New model: A model with a ground-truth circuit
- Standard datasets and counterfactuals: Tasks and causal variables of varying difficulties and required reasoning types
- Novel scientific insights: Edge-level circuits outperform node-level; attribution and mask learning methods are best for circuit discovery; DAS performs well and establishes that there are linear features that realize causal variables, but standard dimensions of hidden vectors are better units of analysis than SAE features.
Motivation
Types of MI Methods
We view most MI methods as performing either localization or featurization (or both). We split these two functions into two tracks: the circuit localization track, and the causal variable track.Materials
Data
Both tracks evaluate across four tasks. These are selected to represent various reasoning types, difficulty levels, and answer formats.- Indirect Object Identification (IOI)
- Multiple-choice Question Answering (MCQA)
- Arithmetic
- AI2 Reasoning Challenge (ARC)
Models
We include models of diverse capability levels and sizes:- GPT-2 Small
- Qwen-2.5 (0.5B)
- Gemma-2 (2B)
- Llama-3.1 (8B)
Circuit Localization Track
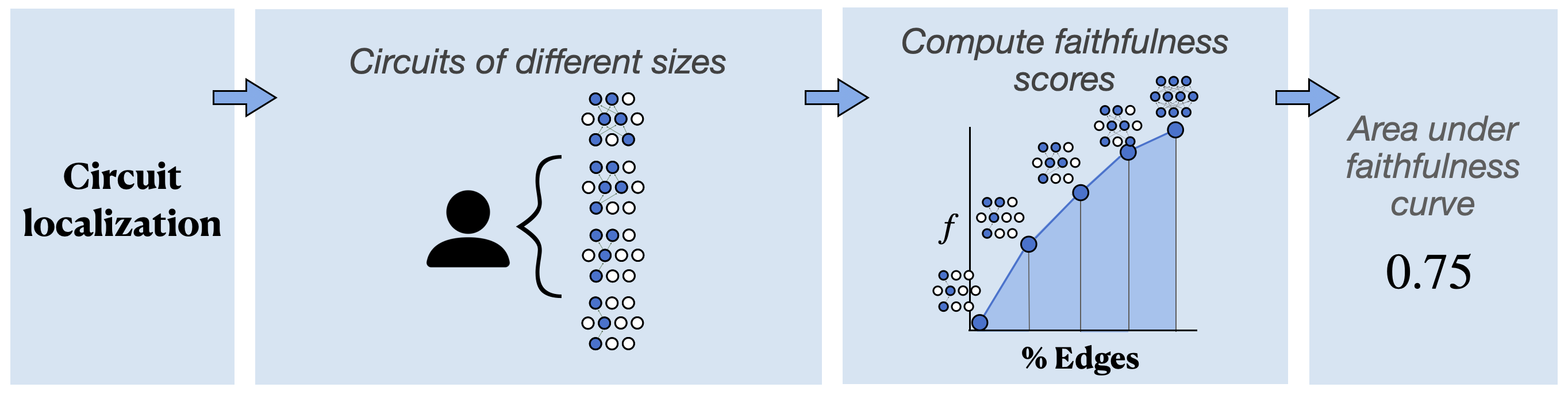
Metrics
Past circuit discovery work often uses faithfulness. This is good for measuring the quality of a single circuit, but how do we measure the quality of a circuit discovery method?Furthermore, people often mean one of two things by this: (i) the subgraph that is responsible for performing the task well, or (ii) the smallest subgraph that replicates the model's behavior (including its failures).
Thus, we propose two metrics: the integrated circuit performance ratio (CPR; higher is better), and the integrated circuit-model difference (CMD; 0 is best). CPR is basically the area under the faithfulness curve at many circuit sizes. CMD is the area between the faithfulness curve and 1, where 1 indicates that the circuit and model have the exact same task behavior (with respect to what is being measured).
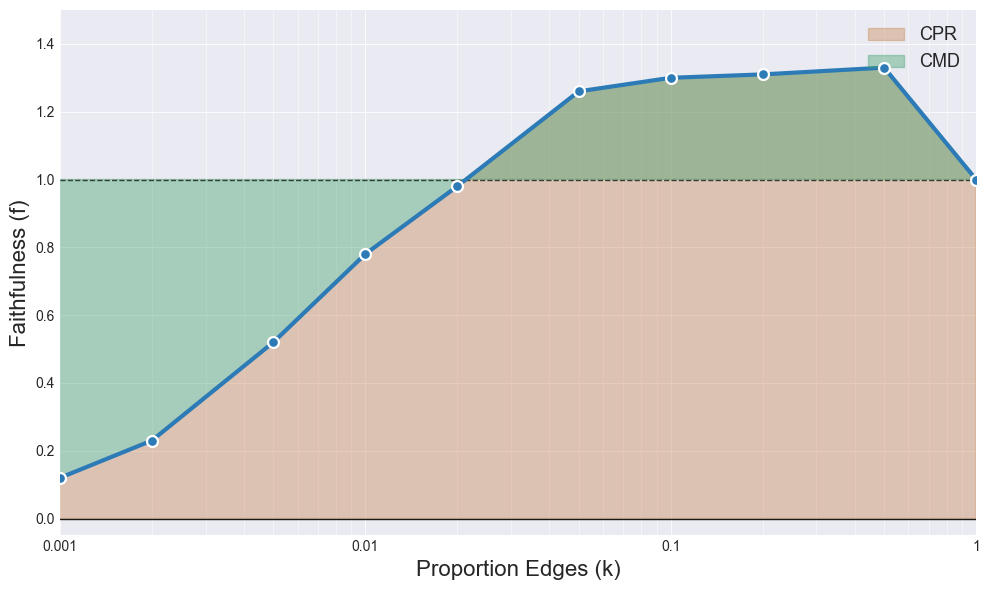
An issue with faithfulness is that it's not clear what the lower or upper bounds are. Thus, we include a fifth model for this track: an InterpBench model. This is a model that we train to contain a known ground-truth circuit. Because we know what the edges are, we can compute the AUROC over the edges at many circuit sizes.
Baselines
We evaluate a variety of methods, including:- Activation patching
- Gradient attribution methods
- Mask learning methods
- Information flow routes
- Edge-level and node-level circuit discovery
Results
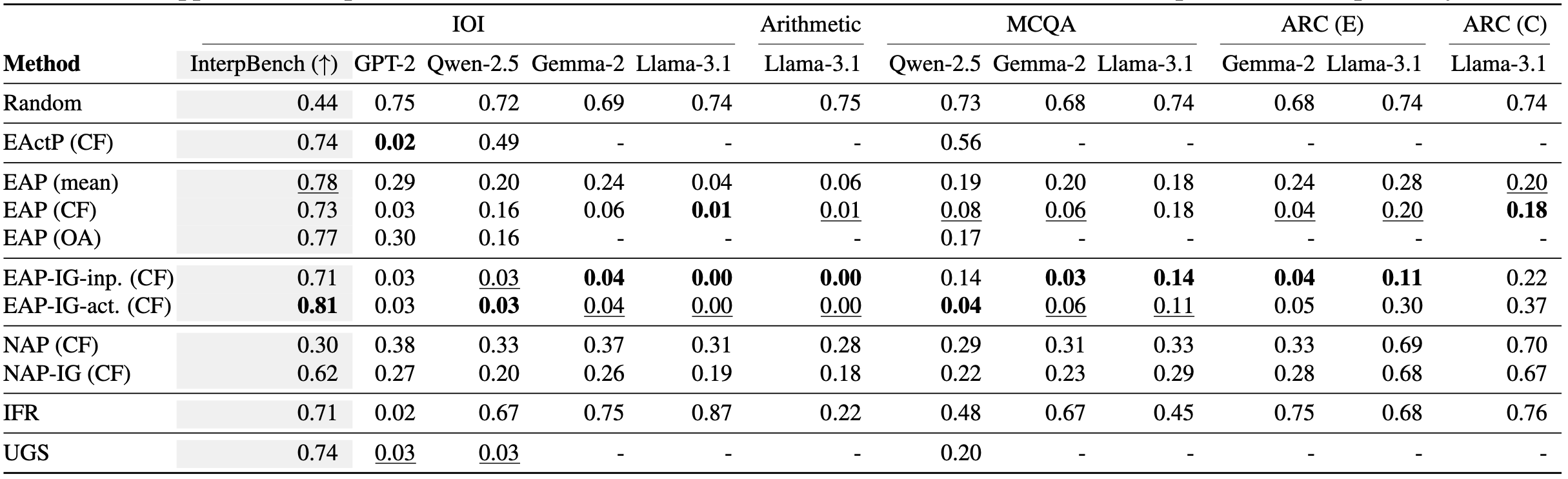
 Attribution patching with integrated gradients (*AP-IG) outperforms attribution patching (*AP), and most other
methods.
Attribution patching with integrated gradients (*AP-IG) outperforms attribution patching (*AP), and most other
methods. Edge-level circuits (E*) outperform node-level circuits (A*).
Edge-level circuits (E*) outperform node-level circuits (A*). Patching with activations from counterfactual inputs (CF) outperforms
other common patching methods.
Patching with activations from counterfactual inputs (CF) outperforms
other common patching methods. UGS, a mask-learning method, performs well.
UGS, a mask-learning method, performs well.Causal Variable Localization Track
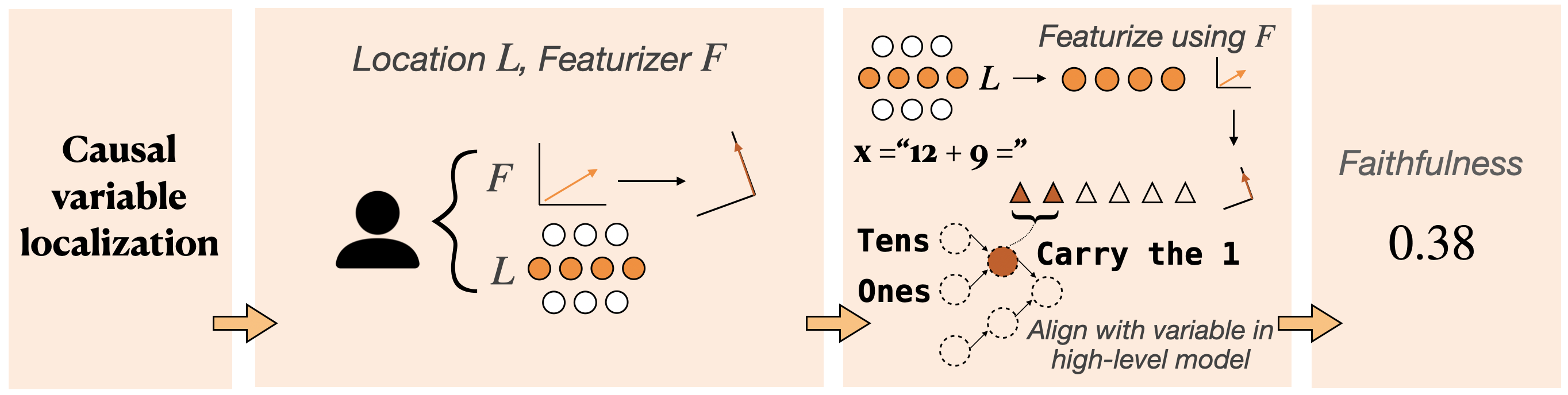
Submissions
A submission will align a causal variable in a model that solves the task with features of a hidden vector. For each layer, a submission can provide a hidden vector, a featurizer, and a set of features the variable is aligned to.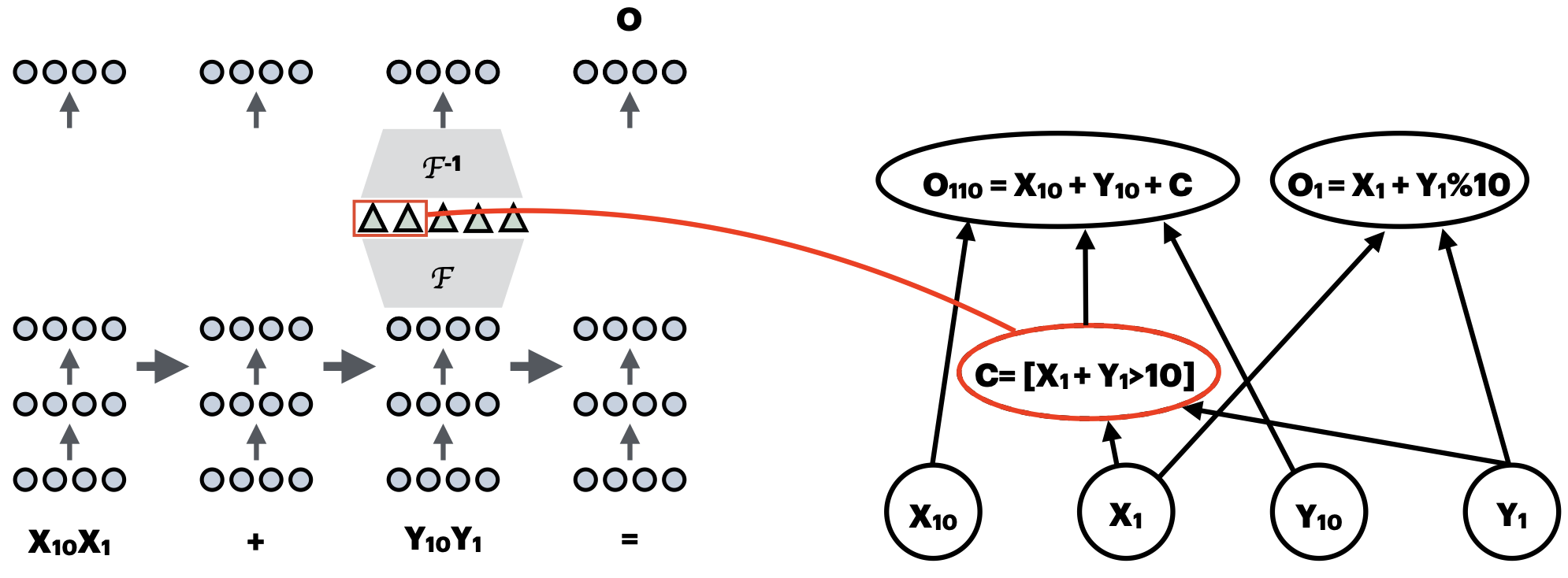
Metrics
We want to evaluate the quality of a featurizer, a transformation of the activations that makes it easier to isolate the desired causal variable. For this, we typically use interchange intervention accuracy.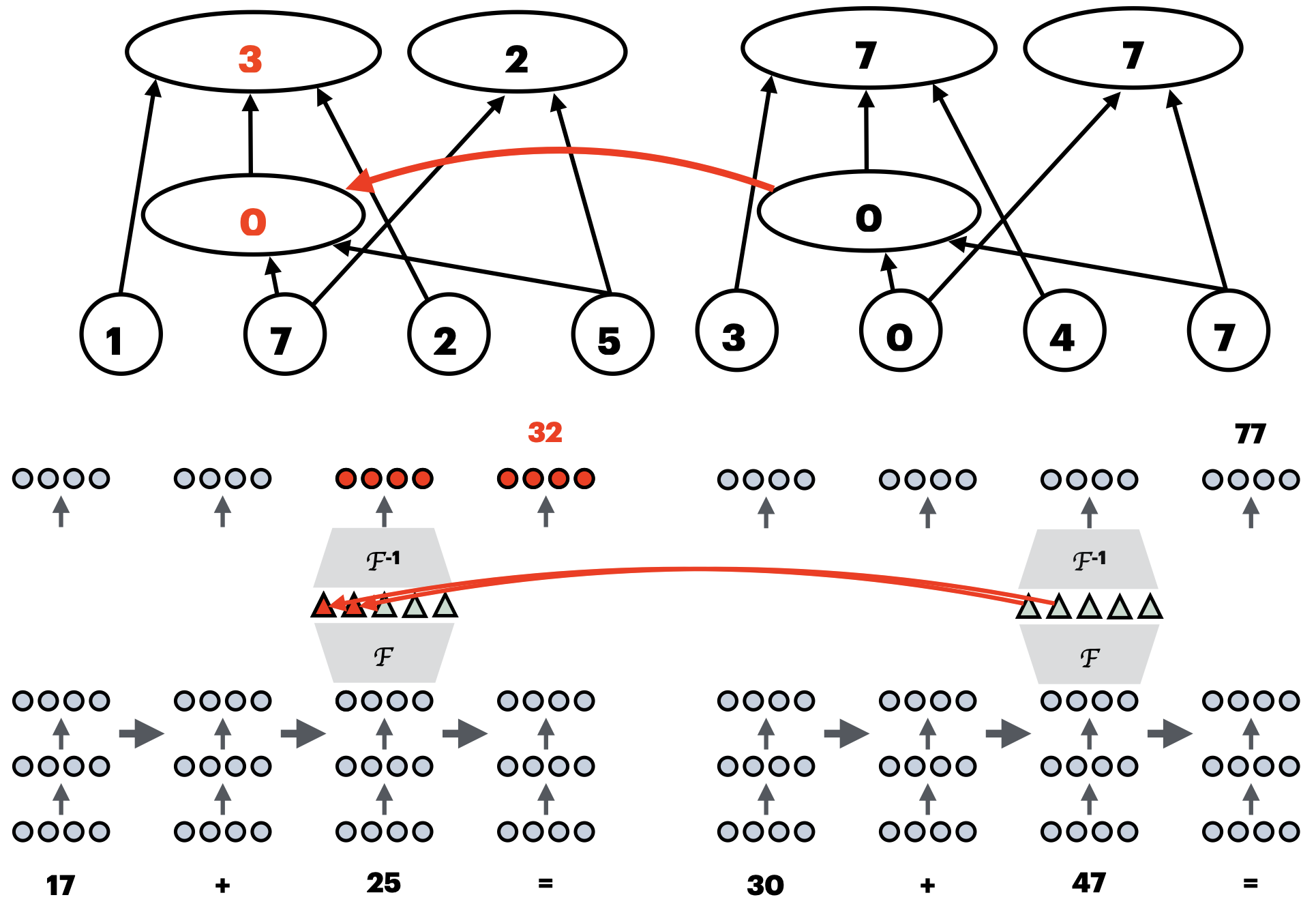
Baselines
We evaluate a mixture of supervised and unsupervised, as well as parametric and non-parametric, methods.- Distributed alignment search (DAS)
- Differentiable binary masks (DBM) on standard dimensions of hidden vectors
- DBM on Sparse autoencoder (SAE) features
- DBM on Principal component analysis (PCA) features, i.e., principal components
Results
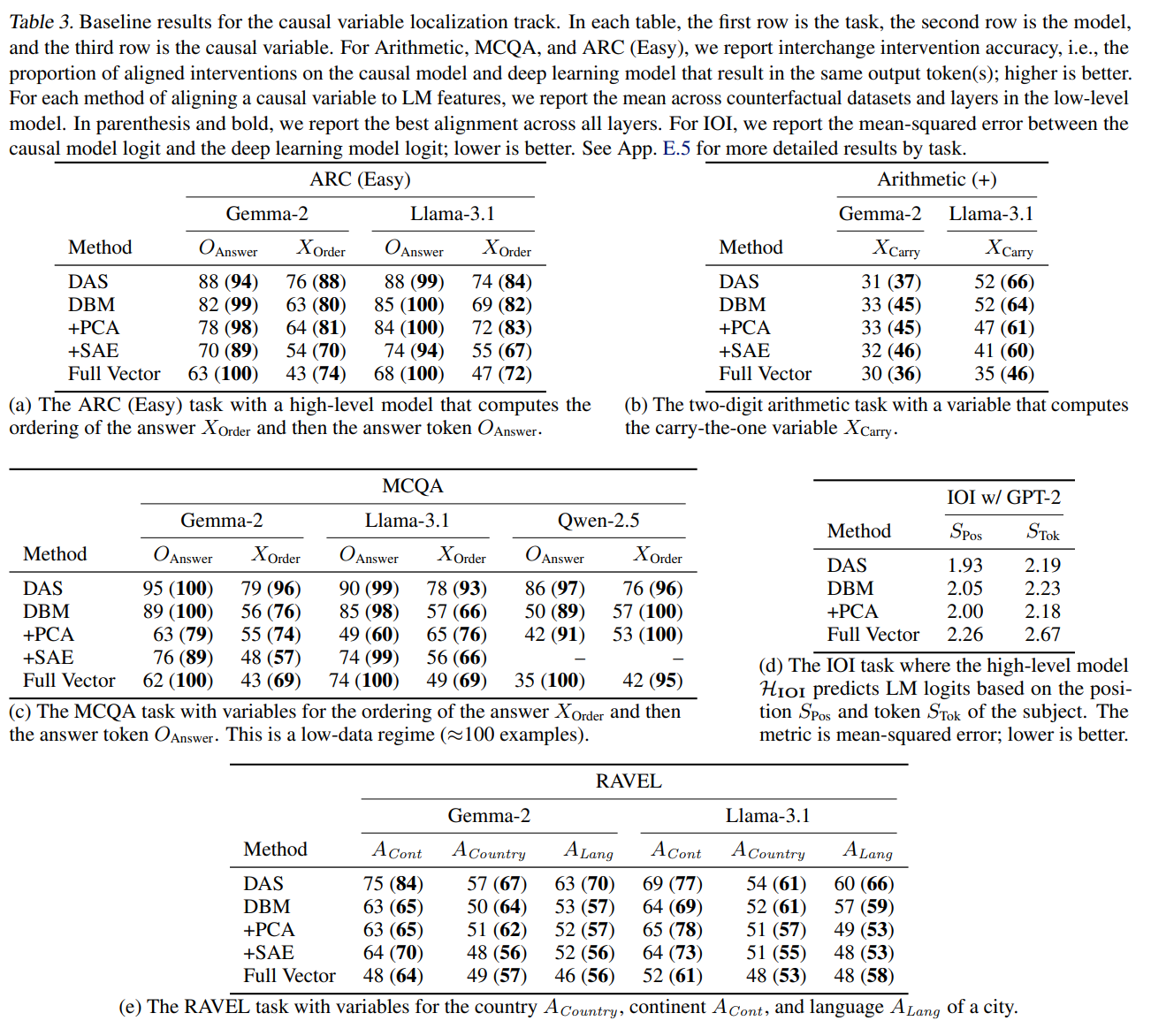
 The supervised features from DAS generally performs best.
The supervised features from DAS generally performs best. Learning masks over basis-aligned dimensions of hidden vectors and principal components are also strong methods.
Learning masks over basis-aligned dimensions of hidden vectors and principal components are also strong methods. SAEs fail to provide a better unit of analysis than basis-aligned dimensions, except for the RAVEL task for the continent causal variable in the Gemma-2 model.
SAEs fail to provide a better unit of analysis than basis-aligned dimensions, except for the RAVEL task for the continent causal variable in the Gemma-2 model. SAEs are high-variance: sometimes they approach the performance of the best methods, but sometimes approach that of the worst.
SAEs are high-variance: sometimes they approach the performance of the best methods, but sometimes approach that of the worst.How to cite
bibliography
Aaron Mueller*, Atticus Geiger*, Sarah Wiegreffe, Dana Arad, Iván Arcuschin, Adam Belfki, Yik Siu Chan, Jaden Fiotto-Kaufman, Tal Haklay, Michael Hanna, Jing Huang, Rohan Gupta, Yaniv Nikankin, Hadas Orgad, Nikhil Prakash, Anja Reusch, Aruna Sankaranarayanan, Shun Shao, Alessandro Stolfo, Martin Tutek, Amir Zur, David Bau, Yonatan Belinkov, “MIB: A Mechanistic Interpretability Benchmark”. Proceedings of the Forty-second International Conference on Machine Learning (ICML 2025).
bibtex
@inproceedings{mib-2025,
title = {{MIB}: A Mechanistic Interpretability Benchmark},
author = {Aaron Mueller and Atticus Geiger and Sarah Wiegreffe and Dana Arad and Iv{\'a}n Arcuschin and Adam Belfki and Yik Siu Chan and Jaden Fiotto-Kaufman and Tal Haklay and Michael Hanna and Jing Huang and Rohan Gupta and Yaniv Nikankin and Hadas Orgad and Nikhil Prakash and Anja Reusch and Aruna Sankaranarayanan and Shun Shao and Alessandro Stolfo and Martin Tutek and Amir Zur and David Bau and Yonatan Belinkov},
year = {2025},
booktitle={Forty-second International Conference on Machine Learning},
url = {https://arxiv.org/abs/2504.13151}
}